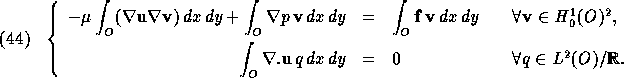
Cette partie aborde la méthode des éléments finis appliquée au problème de Stokes. Le fait de se restreindre au problème de Stokes n'enlève rien à la méthode mais simplifie l'écriture des équations. Pour plus d'information, il est conseillé de se référer au livre de Girault et Raviart [GR86]. On peut aussi regarder le livre de Brezzi et Fortin [BF91].
La formulation variationnelle (appelée faible aussi) du problème de Stokes est obtenue en multipliant les égalités par une fonction test puis en intégrant sur le domaine O. On a ainsi après une intégration par parties :
Cela s'écrit aussi habituellement :
avec a et b les fonctionnelles que l'on déduit de (
).
L'espace quotienté par indique que la pression est
définie à une constante près.
Pour être rigoureux il faudrait parler des conditions aux frontières c.a.d. savoir comment on définit sur . On considère dans cette présentation que l'on a des conditions aux frontières de Dirichlet homogènes (i.e. sur ).
Soit , le problème devient alors trouver tels que :
Ce problème a une solution unique par Lax-Milgram (a est bilinéaire coercive continue et la forme du second membre est linéaire continue).
Soit maintenant et deux espaces de dimension finie approchant
et respectivement .
Le problème () devient trouver tel que :
et avec
on revient au problème suivant :
trouver tels que :
On constate que l'on n'a pas (pour s'en convaincre, imaginez que ). Inversement, si est trop riche, risque d'être vide et donc il n'y a pas de solution. Le problème réside donc à trouver des espaces d'approximation et qui permettent une bonne solution. Cela revient à définir les bons éléments mixtes.
Pour cela il suffit vérifier la condition Inf-Sup discrète qui lie les deux espaces d'approximation :
avec . En pratique, sachant que la condition Inf-Sup continue est vérifiée pour le problème de Stokes, il ne reste plus qu'a vérifier que (cf [BF91])
avec l'opérateur de projection de V sur .
